1. Signal Processing on Cortical Surfaces

 

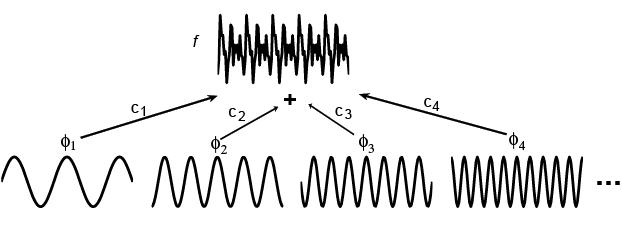
Figure 1.Signal processing in the Euclidean space, such as filtering and signal reconstruction, can be achieved through Fourier bases

 

Signal processing in the Euclidean space, such as filtering and signal reconstruction, can be achieved through Fourier bases as shown in Figure 1. However, such operations cannot be easily done on cortical surfaces.

We like to construct a variety of basis functions on the cortical surfaces, such as ones of the Laplace-Beltrami (LB) operator (see Figure 2 ), such that traditional signal processing methods in the Euclidean space can be extended to the surfaces.

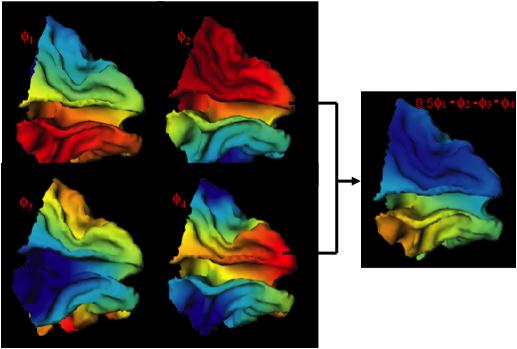
Figure 2.basis functions on the cortical surfaces, such as ones of the Laplace-Beltrami (LB) operator

 

2. Spectral Laplace-Beltrami Wavelets

Download Matlab Toolbox

 

The Spectral Laplace-Beltrami Wavelets is a technique for computing wavelet transforms of functions defined on differentiable and closed 2-manifolds. It is inspired by the Spectral Graph Wavelet Transform (SGWT) from which its capabilities were extended from arbitrary graphs to triangular meshes. The proposed technique replaces the graph-Laplacian with a discretized Laplace-Beltrami operator that captures, in addition to the nodes and edges, geometric information such as the intrinsic curvature of the underlying surfaces.

 



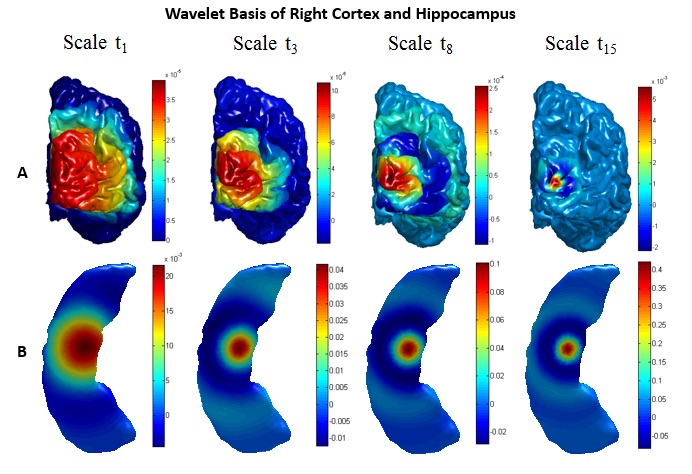
Figure 3. Visualisation of spectral Laplace-Beltrami wavelet bases at decreasing scales (from left to right along each row) on the cortical surface (top row) and hippocampal surface (bottom row).

 



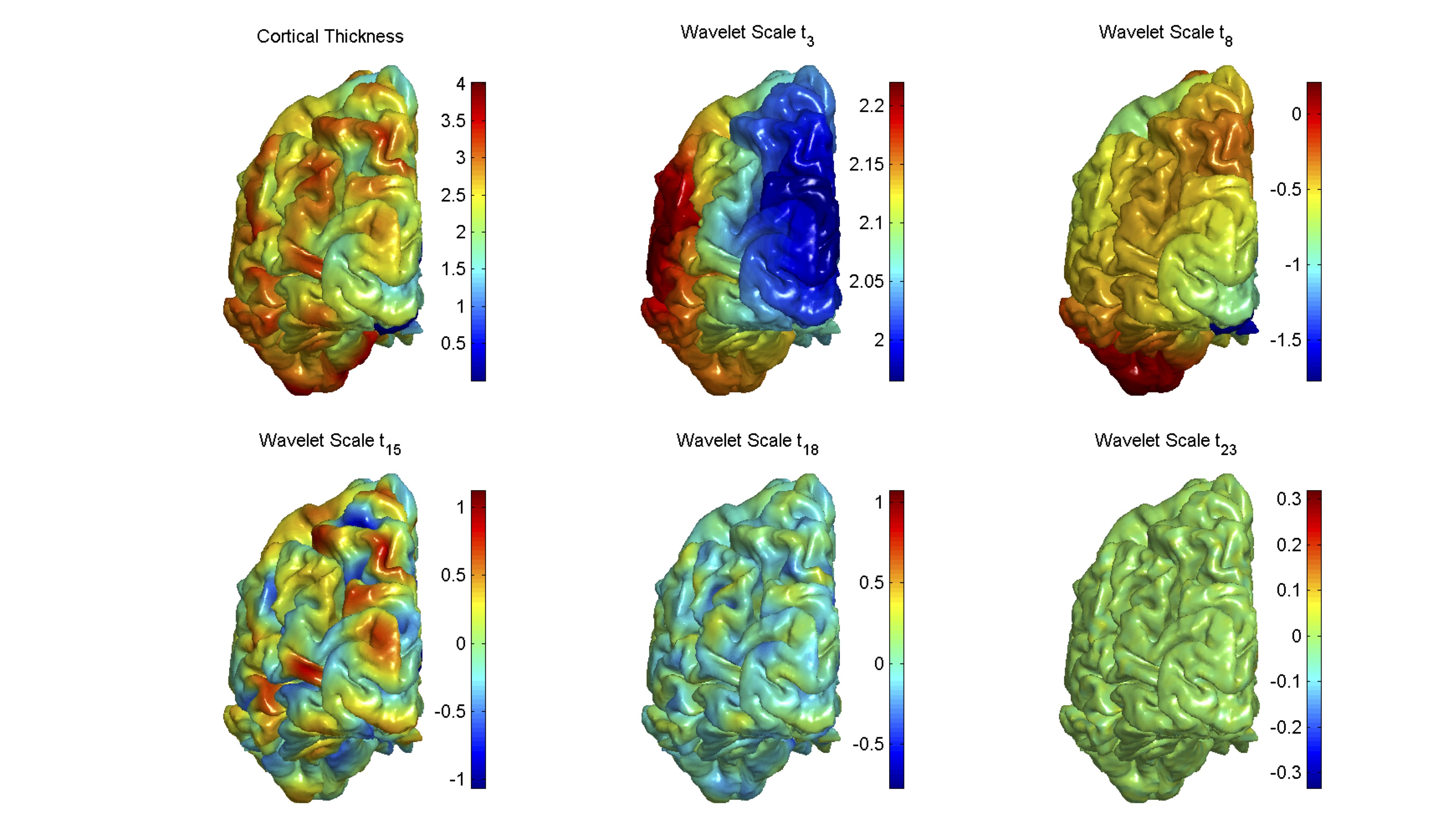
Figure 4.The first panel on the top left is the cortical thickness function plotted on the cortical surface. The subsequent panels show wavelet coefficients at decreasing scales from left to right.

 

Applications: The wavelet coefficients computed can be used to detect high frequency differences (edge detection) or reconstructed with low-pass filters to function as a smoothing operator. Wavelet coefficients, computed at different scales, can also be used as multiresolution input features of pattern recognition/classification algorithms. For example, a classifier constructed from a mix of hippocampi shapes was used to differentiate between normal subjects and those afflicted with Alzheimer’s disease.

 

This toolbox also provides examples for edge detection, wavelet transform, and visualization (see readme.pdf).

 

Reference

[1] Tan, Mingzhen, and Anqi Qiu. "Spectral laplace-beltrami wavelets with applications in medical images." IEEE transactions on medical imaging 34.5 (2015): 1005-1017.

[2] Anqi Qiu*, Dmitri Bitouk, Michael I. Miller, “Smooth Functional and Structural Maps on the Neocortex via Orthonormal Bases of the Laplace-Beltrami Operator”, IEEE Trans. Med. Imaging, 25(10), 1296-1306, 2006.