1. Vertex-based Convolutional Neural Networks
Download Toolbox
We developed a convolution neural network (CNN) on semi-regular triangulated meshes whose vertices have 6 neighbours. The key blocks of the proposed CNN, including convolution and down-sampling, are directly defined in a vertex domain. By exploiting the ordering property of semi-regular meshes, the convolution is defined on a vertex domain with strong motivation from the spatial definition of classic convolution. Moreover, the down-sampling of a semi-regular mesh embedded in a 3D Euclidean space can achieve a down-sampling rate of 4, 16, 64, etc.
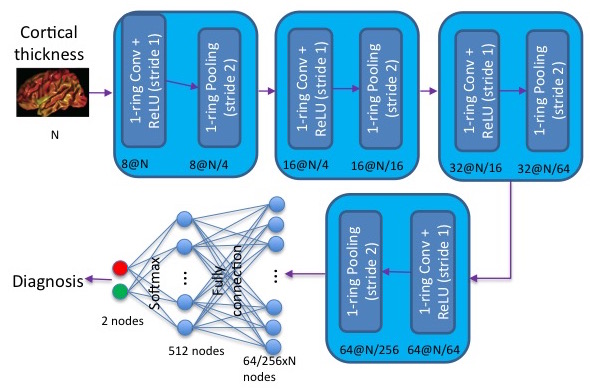
This figure illustrates an example of the architecture of the proposed CNN on a semi-regular triangulated mesh. The four layers respectively include 8, 16, 32, and 64 filters. N represents the number of vertices on the input mesh.
Applications: We demonstrated the use of this vertex-based graph CNN for the classification of mild cognitive impairment (MCI) and Alzheimer's disease (AD) based on 3169 MRI scans of the Alzheimer's Disease Neuroimaging Initiative (ADNI). We showed that this vertex-based graph CNN outperfomed spectral graph CNN.
Reference
[1] Chaoqiang Liu, Hui Ji, Anqi Qiu, Convolutional Neural Network on Semi-Regular Triangulated Meshes and its Application to Brain Image Data.
2. Laplace-Beltrami Convolutional Neural Networks (LB-CNN)
Download Toolbox
We revisit spectral graph convolutional neural networks (graph-CNNs) given in Defferrard (2016) and develops the Laplace-Beltrami CNN (LB-CNN) by replacing the graph Laplacian with the LB operator. We then define spectral filters via the LB operator on a graph. We explore the feasibility of Chebyshev, Laguerre, and Hermite polynomials to approximate LB-based spectral filters and define an update of the LB operator for pooling in the LB-CNN. We employ the brain image data from Alzheimer's Disease Neuroimaging Initiative (ADNI) and demonstrate the use of the proposed LB-CNN. Based on the cortical thickness of the ADNI dataset, we showed that the LB-CNN didn't improve classification accuracy compared to the spectral graph-CNN. The three polynomials had a similar computational cost and showed comparable classification accuracy in the LB-CNN or spectral graph-CNN. Our findings suggest that even though the shapes of the three polynomials are different, deep learning architecture allows us to learn spectral filters such that the classification performance is not dependent on the type of the polynomials or the operators (graph Laplacian and LB operator).
Reference
[1] Shih-Gu Huang, Moo Chung, Anqi Qiu, Revisiting convolutional neural network on graphs with polynomial approximations of Laplace-Beltrami spectral filtering.
3. Fast Mesh Data Augmentation via Chebyshev Polynomial of Spectral filtering
Download Toolbox
Deep neural networks have recently been recognized as one of the powerful learning techniques in computer vision and medical image analysis. Trained deep neural networks need to be generalizable to new data that was not seen before. In practice, there is often insufficient training data available and augmentation is used to expand the dataset. Even though graph convolutional neural network (graph-CNN) has been widely used in deep learning, there is a lack of augmentation methods to generate data on graphs or surfaces. This study proposes two unbiased augmentation methods, Laplace-Beltrami eigenfunction Data Augmentation (LB-eigDA) and Chebyshev polynomial Data Augmentation (C-pDA), to generate new data on surfaces, whose mean is the same as that of real data. LB-eigDA augments data via the resampling of the LB coefficients. In parallel with LB-eigDA, we introduce a fast augmentation approach, C-pDA, that employs a polynomial approximation of LB spectral filters on surfaces. We design LB spectral bandpass filters by Chebyshev polynomial approximation and resample signals filtered via these filters to generate new data on surfaces. We first validate LB-eigDA and C-pDA via simulated data and demonstrate their use for improving classification accuracy. We then employ the brain images of Alzheimer's Disease Neuroimaging Initiative (ADNI) and extract cortical thickness that is represented on the cortical surface to illustrate the use of the two augmentation methods. We demonstrate that augmented cortical thickness has a similar pattern to real data. We also show that C-pDA is faster than LB-eigDA and can improve the AD classification accuracy of graph-CNN.
Reference
[1] Shih-Gu Huang, Moo Chung, Anqi Qiu, Fast Mesh Data Augmentation via Chebyshev Polynomial of Spectral filtering.
